Точка бифуркации
Материал из Викитаки
Точка бифуркации — в общем случае момент времени или точка места, в котором происходит непрогнозируемый переход системы в одно из иных, топологически неэквивалентных исходному, состояний. Критическое фазовое состояние системы, при котором система становится неустойчивой относительно флуктуаций (возмущений) и возникает неопределенность: станет ли состояние системы хаотическим или она перейдет в то или иное новое устойчивое состояние, например, на более дифференцированный и высокий уровень упорядоченности.
Точка бифуркации математически описывается следующим образом:
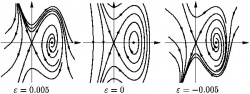
В системе x′ = f(x, ε) точкой локальной бифуркации динамической системы со стационарной точкой x0 является точка ε = 0, если найдутся сколь угодно малые значения ε, при которых динамическая система в окрестности точки x0 не является локально топологически эквивалентной системе, отвечающей нулевому значению параметра.
Математически описаны также бифуркация седло-узла, бифуркация гомоклинической траектории седла или бифуркация петли сепаратрисы седла, бифуркация цикла или бифуркация Пуанкаре—Андронова—Хопфа и ее частные случаи - бифуркация удвоения периода и бифуркация рождения инвариантного тора, когда вокруг потерявшего устойчивость цикла образуется инвариантное многообразие, гомеоморфное тору. В общем случае на этом торе при приближении параметра к нулевому (бифуркационному) значению в бесконечном числе рождаются и умирают длиннопериодические предельные циклы.
Для математического описания прохождения точки бифуркации используются системы дифференциальных уравнений.
Свойства точки бифуркации
- Непрогнозируемость. Обычно точка бифуркации предваряет несколько ветвей аттрактора (устойчивых состояний системы), в одно из которых перейдет система. Однако заранее невозможно предсказать, какой новый аттрактор займёт система. Это связано с природой времени - невозможно так синхронизировать внутренние состояния элементов системы, чтобы достоверно определить, в каких состояниях они будут в момент, когда система достигнет точки бифуркации.
- Точка бифуркации носит как правило кратковременный локальный характер относительно разделямых ею более длительных устойчивых состояний системы.
На основании свойства непрогнозируемости точки бифуркации все события делятся на
- рациональные,
- иррациональные хаотические - имеющие область бифуркаций и область рациональных аттракторов, и
- иррациональные случайные - когда зона бифуркации охватывает все пространство возможных событий.
Для бифуркации рождения цикла возможно как мягкое возбуждение автоколебаний системы, сопровождающее потерю устойчивости стационарной точки системы, так и жесткое, когда фазовая точка, находившаяся в окрестности устойчивого начала координат, быстро "выбрасывается" из окрестности стационарной точки, например в окрестность имеющейся у системы удаленной устойчивой стационарной точки или удаленного устойчивого цикла.
В цикле ОПИ и ДО
В цикле ОПИ и ДО точки бифуркации фигурируют и обсуждаются в следующих романах: