Сюръекция

Материал из Викитаки

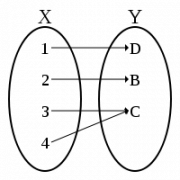
Отображение F:X→Y называется сюръективным (или сюръекцией, или отображением на Y), если каждый элемент множества Y является образом хотя бы одного элемента множества X, то есть ∀y∈Y∃x∈X:y=F(x). Для случая числовых функций это выражается как «функция, принимающая все возможные значения».

Содержание 1 Эквивалентные определения 2 Примеры 3 Использование модели 3.1 В информатике 4 См. также 5 Литература

Эквивалентные определения

Следующие свойства отображения F:X→Y эквивалентны:

1. F сюръективно
2. каждый элемент множества Y имеет хотя бы один прообраз во множестве X при отображении F.
3. образ множества X при отображении F(X) совпадает с Y
4. F имеет правое обратное отображение, то есть такое отображение G:Y→X, что F(G(y))=y для любого y∈Y.

Примеры

1. F:ℝ→[-1;1],F(x)=sin x — сюръективно.
2. F:ℝ→ℝ₊,F(x)=x² — сюръективно.
3. F:ℝ→ℝ,F(x)=x² — не является сюръективным (например, не существует такого x∈ℝ, что F(x)=-9.

Использование модели

В информатике

Организация связи «многие к одному» между таблицами реляционной БД на основе первичных ключей.

См. также

• Функция
• Инъекция
• Биекция

Литература

• Н. К. Верещагин, А.ШеньНачала теории множеств // Лекции по математической логике и теории алгоритмов.
• Ершов Ю. Л., Палютин Е. А.Математическая логика: Учебное пособие. — 3-е, стереотип. изд.. — СПб.: Лань, 2004. — 336 с.